5.6.1 结构的动力分析宜对整体结构按时程分析法进行。条件不具备时,对于矩形建筑物,构件可按作用的爆炸荷载进行动力分析。当按等效静荷载法进行结构动力分析时,对屋面板、外墙等结构构件,宜分别按单独的等效单自由度体系进行动力分析。 5.6.2 钢筋混凝土结构构件,宜按弹塑性工作阶段设计。对于受弯构件,其抗剪承载力应高于抗弯承载力20%。 5.6.3 在爆炸荷载作用下,结构构件的延性比可按下列公式确定: 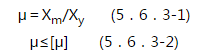 Xm——结构构件弹塑性变位(mm); Xy——结构构件弹性极限变位(mm); [μ]——结构构件的允许延性比,按表5.6.3采用。 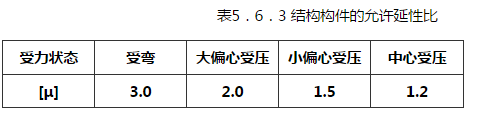 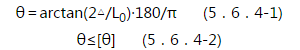 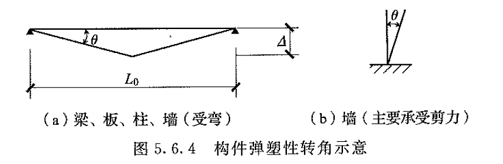 △——跨中变形(mm); L0——构件跨度(mm); [θ]——结构构件的弹塑性转角允许值,按表5.6.4采用。 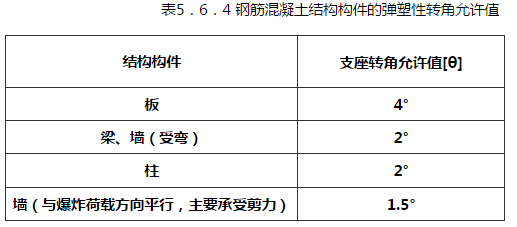 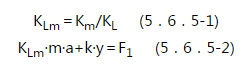 Km——质量传递系数,计算方法按本规范附录B采用; KL——荷载或刚度传递系数,计算方法按本规范附录B采用; m——构件质量(kg); a——质点运动加速度(m/s2); k——构件刚度,计算方法按本规范附录A采用; y——质点位移(m); F1——作用在构件上的力(时间的函数)(N)。 5.6.6 采用单自由度体系进行构件的弹塑性动力分析时,其等效质量和振动周期可按下列公式计算: 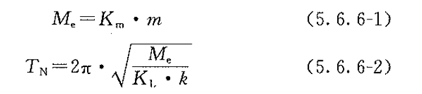 TN——质点振动周期(s)。 5.6.7 构件截面平均惯性矩应按下列公式计算: 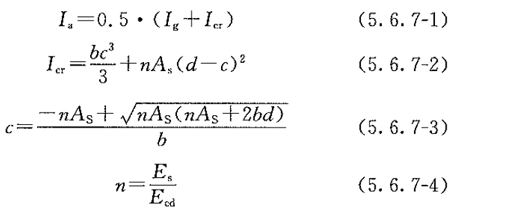 Ig——混凝土构件对形心轴的毛截面惯性矩,不计钢筋影响(mm4); Icr——混凝土开裂截面惯性矩(mm4); b——构件截面宽度(mm); d——构件截面有效高度(mm); As——构件配筋面积(mm2); Es——钢筋弹性模量(N/mm2); Ecd——混凝土动弹性模量,可取静荷载作用时的1.2倍(N/mm2)。 条文说明
5.6.2 为了满足抗爆结构的塑性变形能力,设计时应保证构件首先出现受弯裂缝和钢筋屈服,防止过早地发生斜裂缝破坏,即为抗剪留出稍大的安全储备。
5.6.3 本条参考了现行国家标准《人民防空地下室设计规范》GB 50038中有关钢筋混凝土构件容许延性比的相关规定。该规范一般按表1取值。 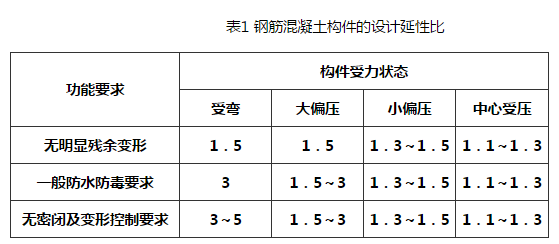 美国混凝土协会Code Requirements for Nuclear Safety Related Concrete Structures(ACI 349)中对容许延性比以及塑性转角的规定如下: 延性比μ是构件最大允许位移Xm与有效屈服点位移Xy的比值,见图4。为了得到有效屈服位移,构件截面惯性矩应取0.5(Ig+Icr)。构件之最大变形不应降低构件的使用功能,同时不能削弱相关系统及部件的安全性。对于梁(次梁)、墙、板等受弯构件,容许延性比可取0.05/(ρ-ρ′)且不超过10,但为在冲击荷载时保证结构整体性其延性比不应大于3.0。 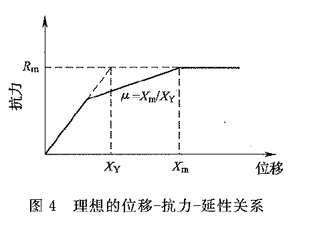 从钢筋混凝土构件的工作过程来看,在荷载的作用下,随着构件挠曲,全部钢筋屈服;钢筋在达到屈服阶段内,当挠度发展到相当于2°支座转角时,受压混凝土被压碎。 5.6.7 确定混凝土构件的挠度无论在弹性或是在塑性范围内都是十分复杂的。这是因为,由于裂缝的开展,构件横截面的有效惯性矩沿构件是连续的;还因为混凝土的弹性模量随应力增长而变化,使问题变得更加复杂。因此变形计算中使用平均惯性矩。通常的做法是先假定构件的配筋As,核算构件的延性比、转角是否满足要求。 |
Powered by Discuz! X3.5
© 2001-2025 Discuz! Team.