4.1.1 当隔振体系为单自由度时,质量中心处的振动位移可按下列公式计算:
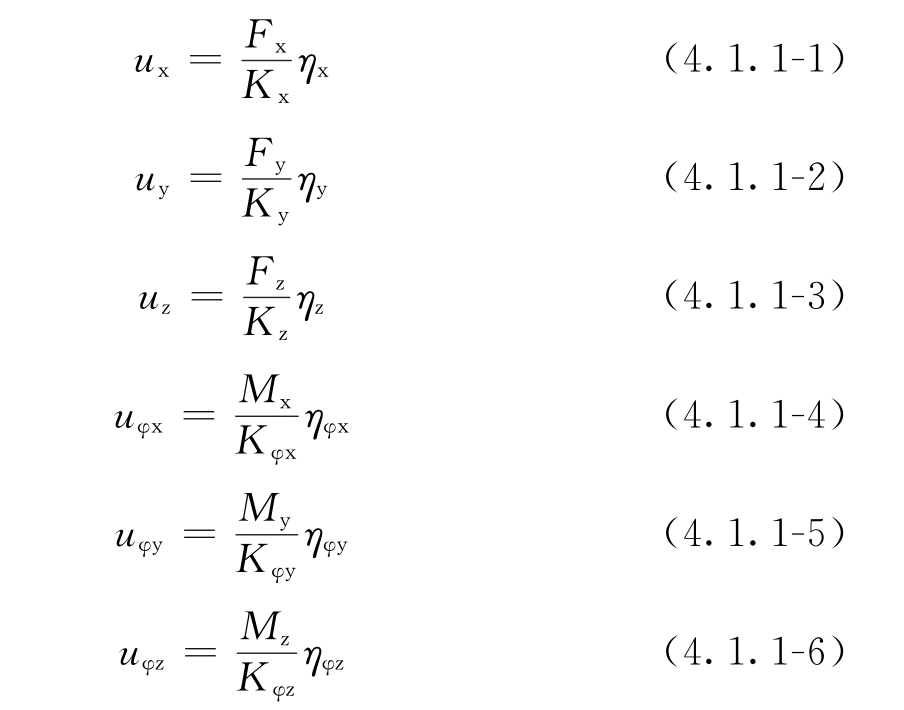 uy——隔振体系质量中心处沿y轴向的振动位移(m); uz——隔振体系质量中心处沿z轴向的振动位移(m); uφx——隔振体系质量中心处绕x轴旋转的振动角位移(rad); uφy——隔振体系质量中心处绕y轴旋转的振动角位移(rad); uφz——隔振体系质量中心处绕z轴旋转的振动角位移(rad); Fx——作用在隔振体系质量中心处沿x轴向的扰力(N); Fy——作用在隔振体系质量中心处沿y轴向的扰力(N); Fz——作用在隔振体系质量中心处沿z轴向的扰力(N); Mx——作用在隔振体系质量中心处绕x轴的扰力矩(N·m); My——作用在隔振体系质量中心处绕y轴的扰力矩(N·m); Mz——作用在隔振体系质量中心处绕z轴的扰力矩(N·m); ηx——单自由度隔振体系沿x轴向的传递率; ηy——单自由度隔振体系沿y轴向的传递率; ηz——单自由度隔振体系沿z轴向的传递率; ηφx——单自由度隔振体系绕x轴旋转的传递率; ηφy——单自由度隔振体系绕y轴旋转的传递率; ηφz——单自由度隔振体系绕z轴旋转的传递率。 4.1.2 当隔振体系为双自由度耦合振动时,质量中心处的振动位移宜按下列规定计算: 1 当x—φy耦合振动时,宜按下列公式计算: 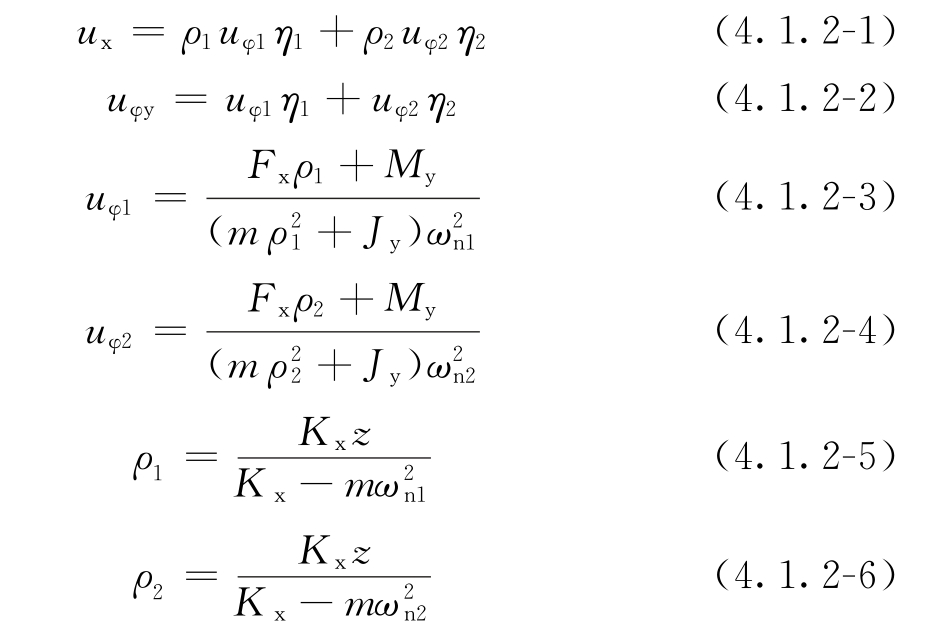 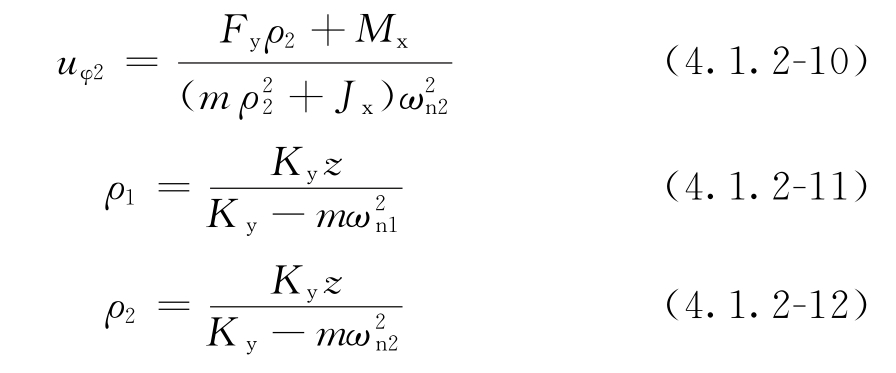 uφ2——隔振体系耦合振动第二振型的当量角位移(rad); ρ1——隔振体系耦合振动第一振型中的水平位移与转角的比值(m/rad); ρ2——隔振体系耦合振动第二振型中的水平位移与转角的比值(m/rad); η1——双自由度隔振体系第一振型的传递率; η2——双自由度隔振体系第二振型的传递率。 4.1.3 隔振体系的传递率宜符合下列规定: 1 当扰力、扰力矩为简谐作用时,传递率宜按下列公式计算: 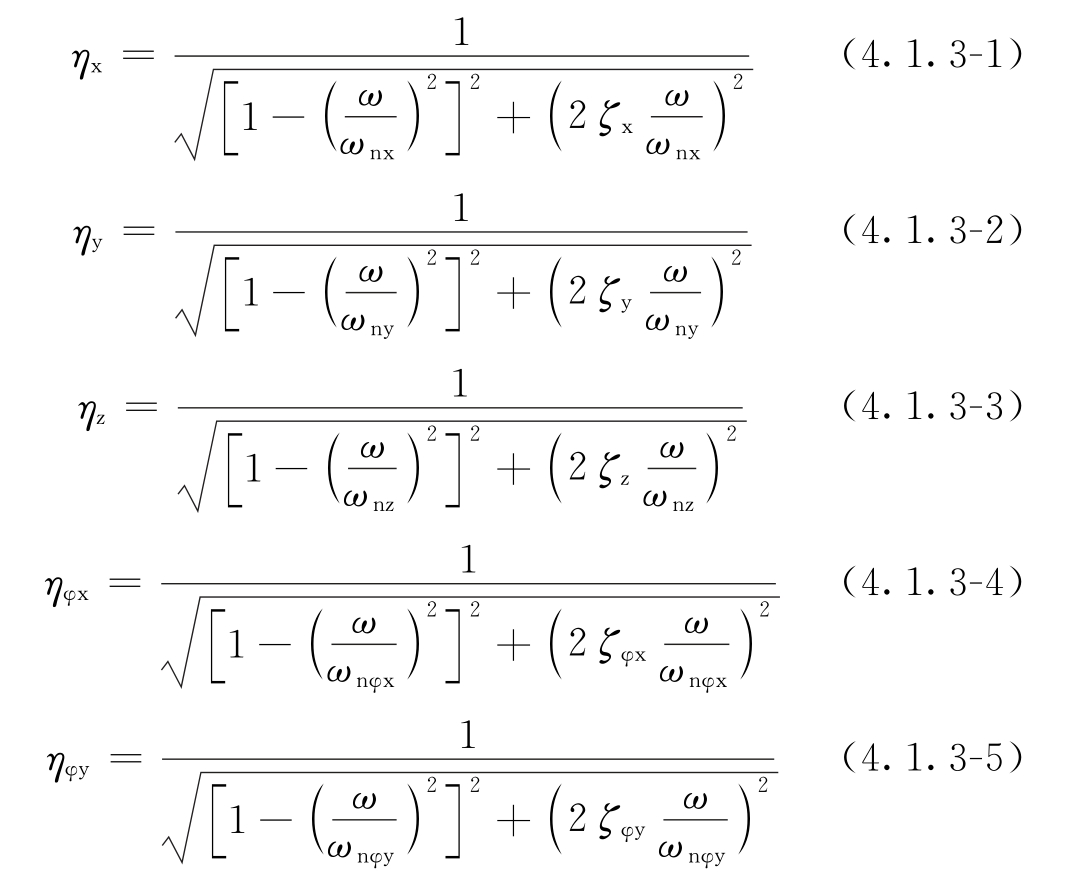  式中:ζx——隔振系统沿x轴向振动的阻尼比; ζy——隔振系统沿y轴向振动的阻尼比; ζz——隔振系统沿z轴向振动的阻尼比; ζφx——隔振系统绕x轴旋转振动的阻尼比; ζφy——隔振系统绕y轴旋转振动的阻尼比; ζφz——隔振系统绕z轴旋转振动的阻尼比; ζ1——两自由度隔振体系第一振型的阻尼比; ζ2——两自由度隔振体系第二振型的阻尼比; ζxi——第i个隔振器沿x轴向振动的阻尼比; ζyi——第i个隔振器沿y轴向振动的阻尼比; ζzi——第i个隔振器沿z轴向振动的阻尼比; ωnx——隔振体系沿x轴向的无阻尼固有圆频率; ωny——隔振体系沿y轴向的无阻尼固有圆频率; ωnz——隔振体系沿z轴向的无阻尼固有圆频率; ωnφx——隔振体系绕x轴旋转的无阻尼固有圆频率; ωnφy——隔振体系绕y轴旋转的无阻尼固有圆频率; ωnφz——隔振体系绕z轴旋转的无阻尼固有圆频率。 2 当为后峰齿形脉冲、对称三角形脉冲、矩形脉冲、正弦半波脉冲和正矢脉冲等冲击作用时,传递率宜按本标准附录A确定。 4.1.4 双自由度隔振体系第一、第二振型的阻尼比宜符合下列规定: 1 当x—φy耦合振动时,宜按下列规定确定: 1)第一振型的阻尼比,可取隔振器沿x轴向振动的阻尼比与隔振器绕y轴旋转振动的阻尼比二者较小值; 2)第二振型的阻尼比,可取隔振器沿x轴向振动的阻尼比与隔振器绕y轴旋转振动的阻尼比二者较大值。 2 当y—φx耦合振动时,宜按下列规定确定: 1)第一振型的阻尼比,可取隔振器沿y轴向振动的阻尼比与隔振器绕x轴旋转振动的阻尼比二者较小值; 2)第二振型的阻尼比,可取隔振器沿y轴向振动的阻尼比与隔振器绕x轴旋转振动的阻尼比二者较大值。 4.1.5 任意点的振动位移的计算应符合下列规定: 1 当作用在隔振体系质量中心处沿各轴向的简谐扰力和绕各轴的简谐扰力矩的工作频率均相同且在作用时间上没有相位差时,任意点的振动位移,可按下列公式计算: 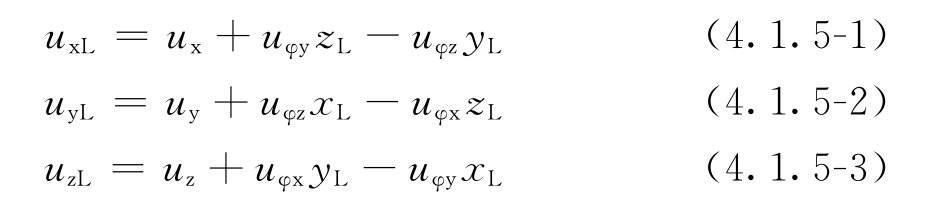 式中:uxL——隔振体系任意点沿x轴向的振动位移(m); uyL——隔振体系任意点沿y轴向的振动位移(m); uzL——隔振体系任意点沿z轴向的振动位移(m); xL——任意点的x轴坐标值(m); yL——任意点的y轴坐标值(m); zL——任意点的z轴坐标值(m)。 2 当作用在隔振体系质量中心处沿各轴向的简谐扰力和绕各轴的简谐扰力矩的工作频率均相同且在作用时间上有相位差时,任意点的振动位移,应计入相位差的影响。 3 当作用在隔振体系质量中心处沿各轴向的简谐扰力和绕各轴的简谐扰力矩的工作频率均不相同时,任意点各轴向的最大振动位移,可按下列公式计算: 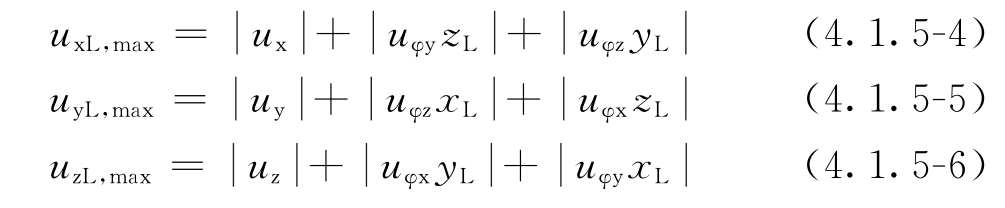 uyL,max——隔振体系任意点沿y轴向的最大振动位移(m); uzL,max——隔振体系任意点沿z轴向的最大振动位移(m)。 4 当扰力、扰力矩为脉冲作用时,任意点处的振动位移可按本条式(4.1.5-1)~式(4.1.5-3)进行计算。 条文说明
4.1.1 当扰力为简谐时间函数(稳态振动)时,如图4所示的主动隔振体系,在扰力Fz(t)=Fzsinωt作用下,其运动微分方程为:
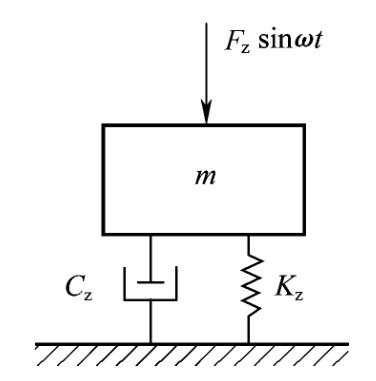 图4 主动隔振体系 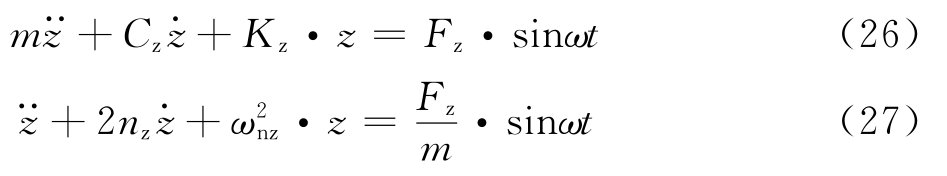 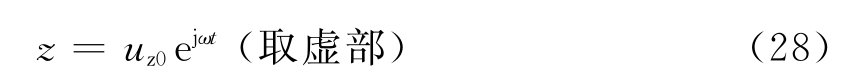 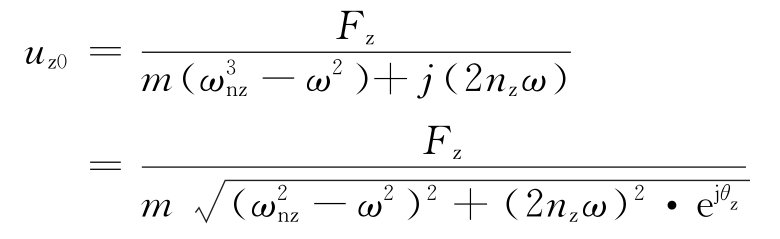 代入式(28)得位移方程: 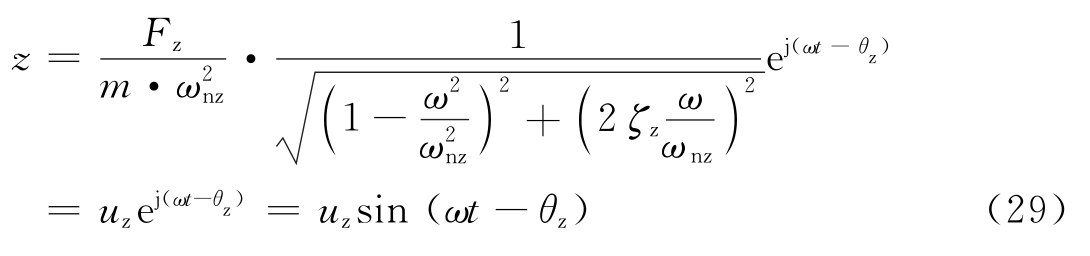 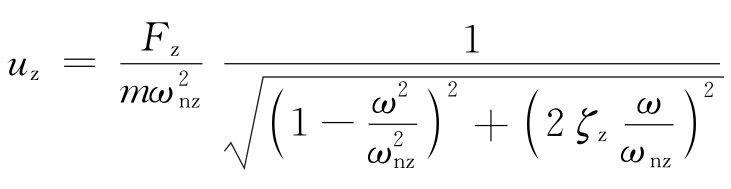 ; ;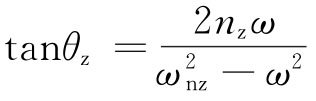 ; ;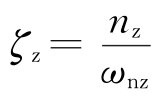 ; ;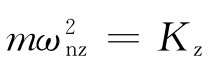 ; ;当sin(ωt-θz)=1时,振动最大,此时振幅值为: 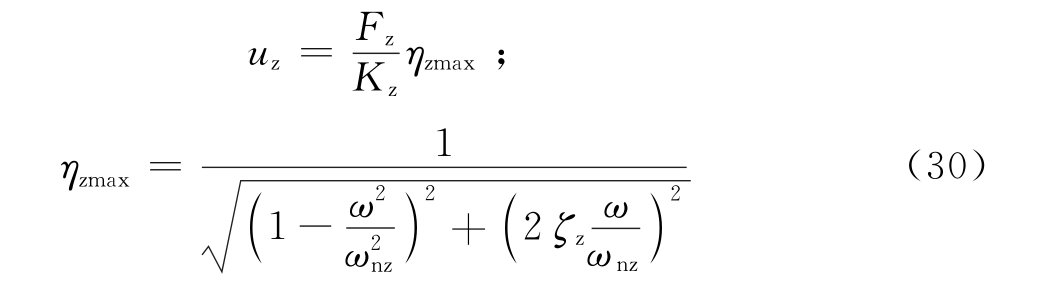 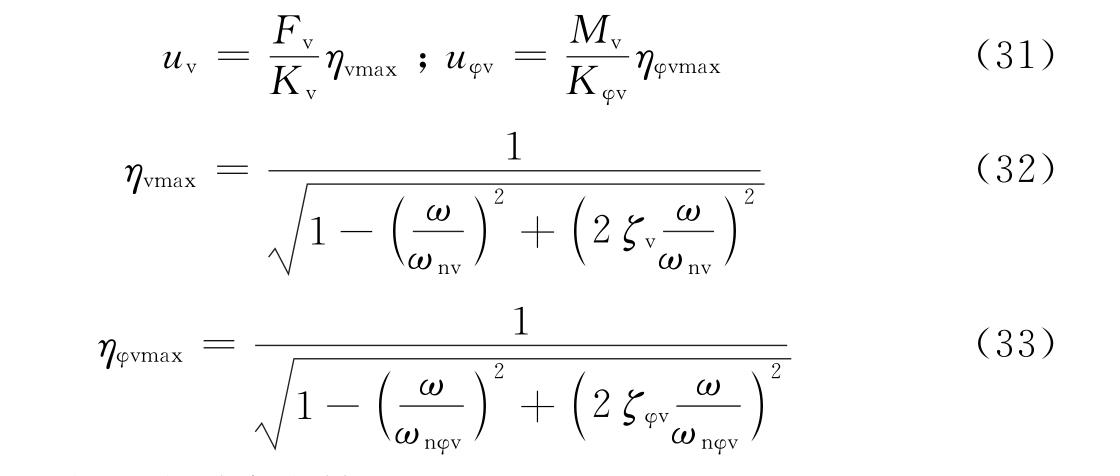 阻尼比可按下列规定进行计算: 当n个阻尼器并联时(图5),其阻尼系数分别为:Cz1、Cz2、…、Czn,在扰力Fz作用线通过刚度中心时,设块体的运动速度为 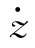 ,则: ,则:
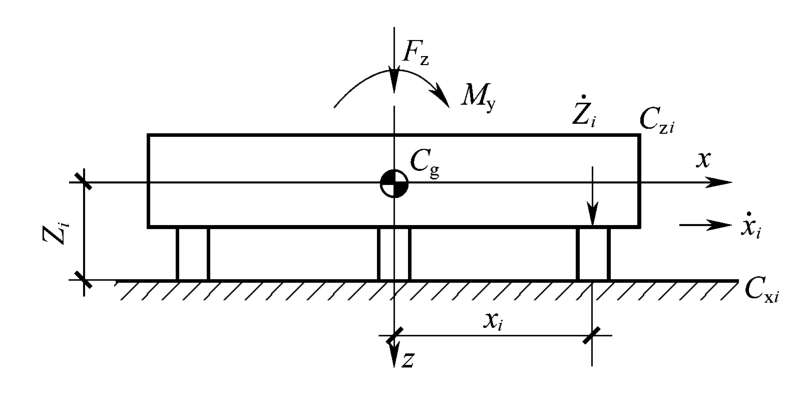 图5 个阻尼器并联的隔振体系 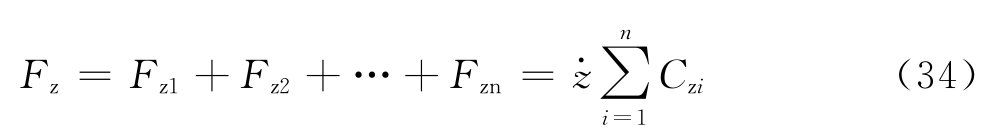 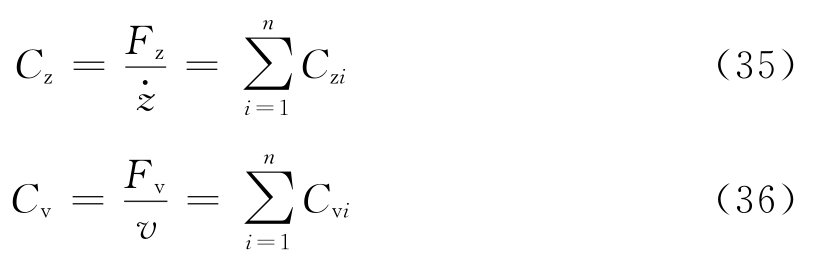 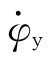 ,第i个阻尼器上端沿x轴向的变位速度分别为: ,第i个阻尼器上端沿x轴向的变位速度分别为: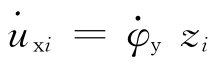 , ,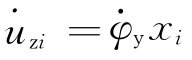 。 。阻尼器所受的阻力分别为: 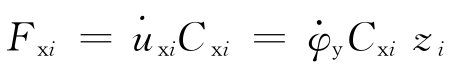 ; ;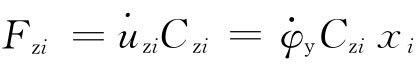 。 。当质心的阻力矩为: 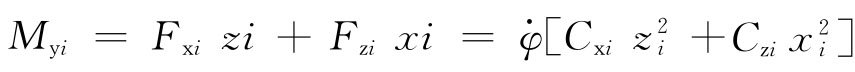 所有阻尼器对绕通过质心的y轴旋转的总阻力矩为: 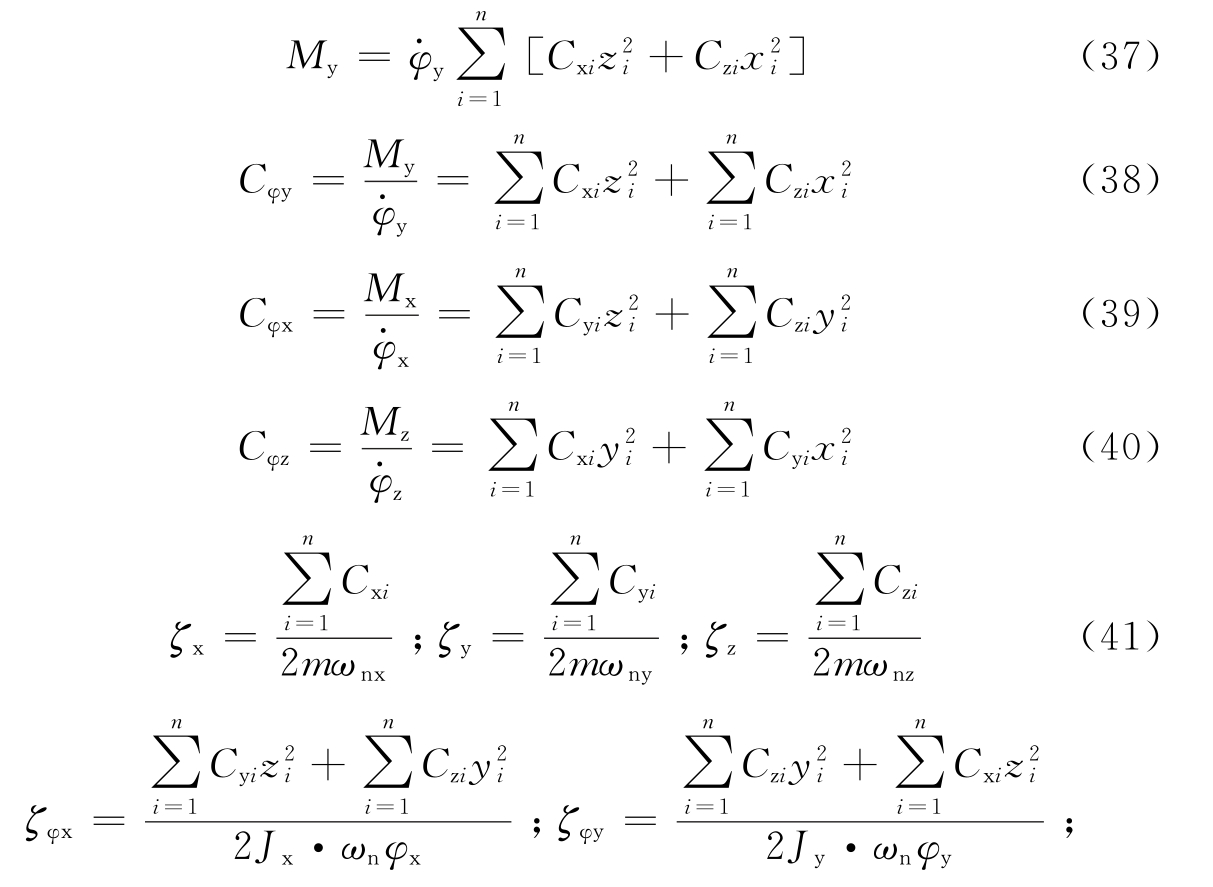 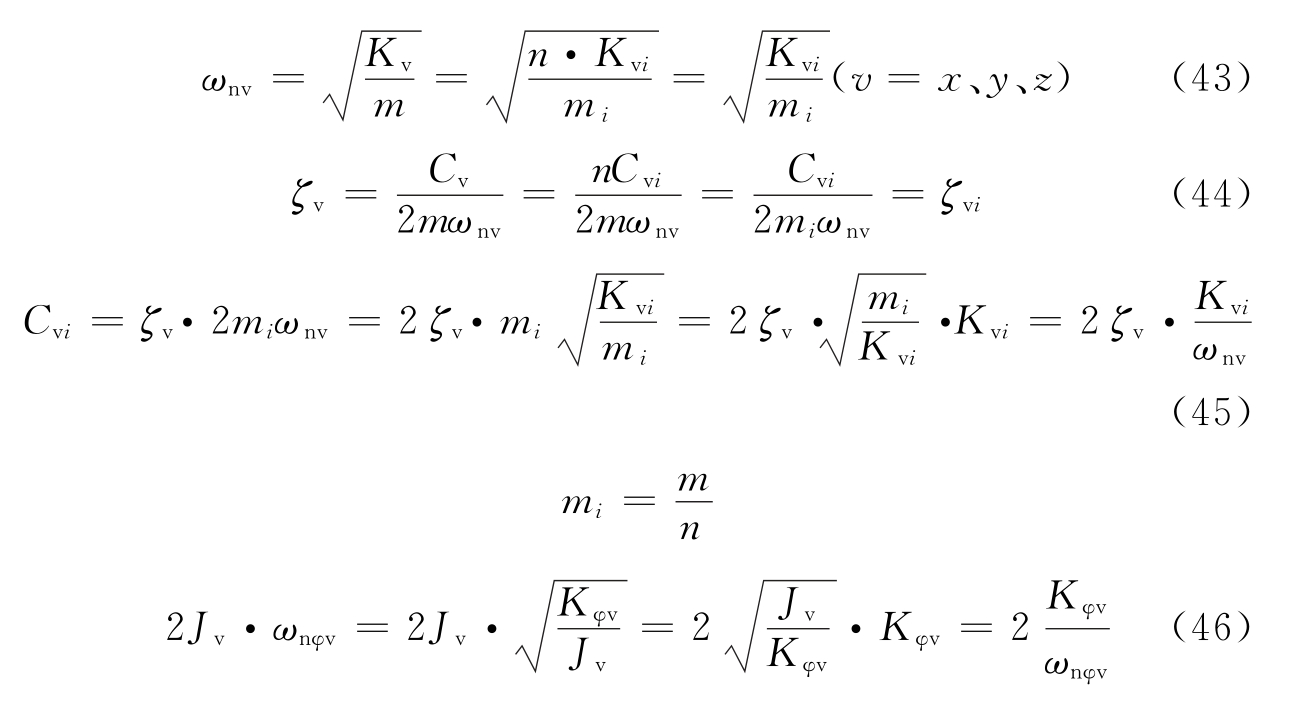 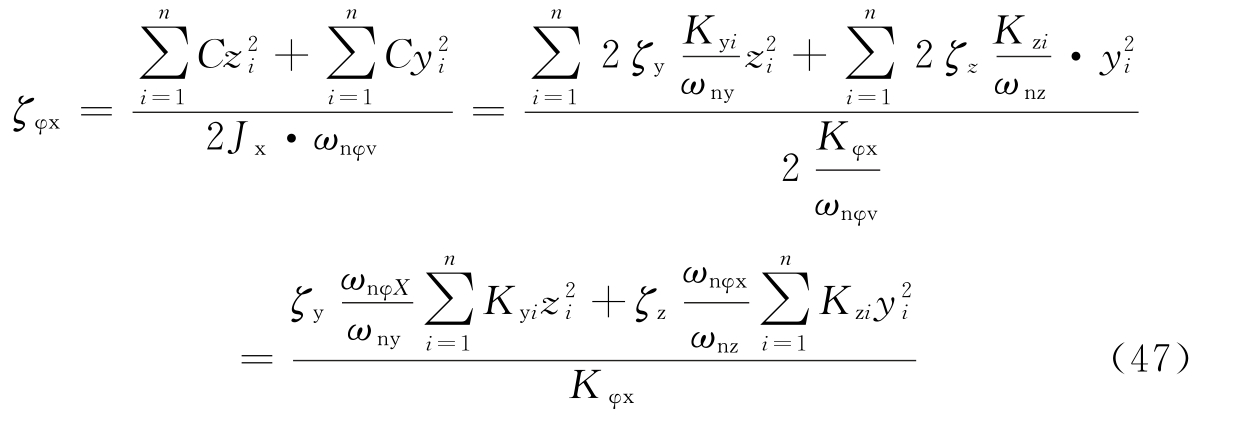 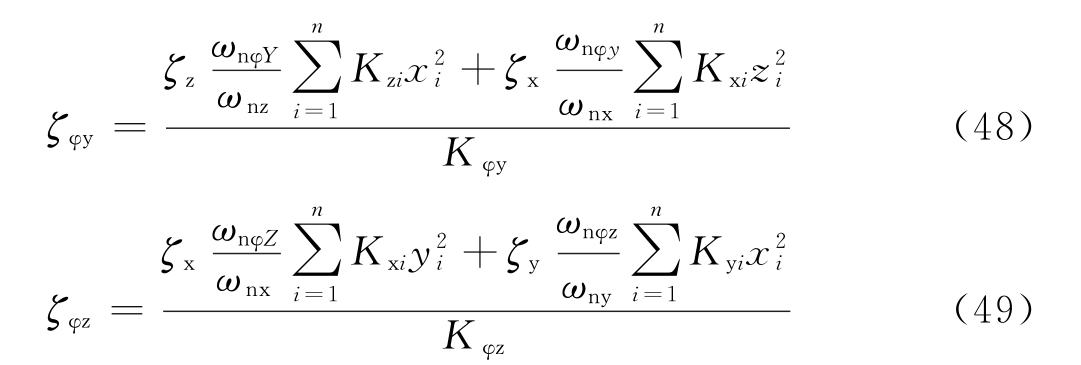 4.1.2 双自由度耦合时的振动位移计算公式推导如下: 对于有阻尼的强迫振动,其微分方程为: 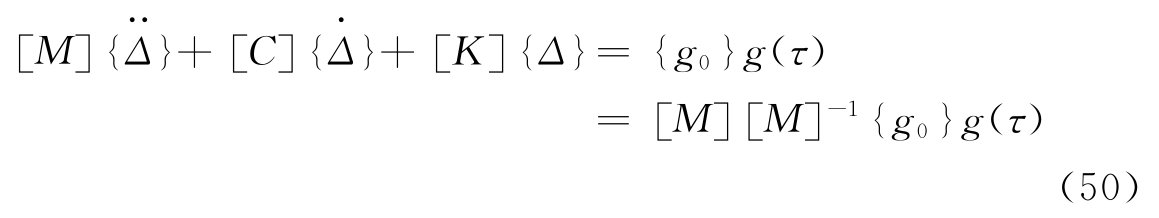 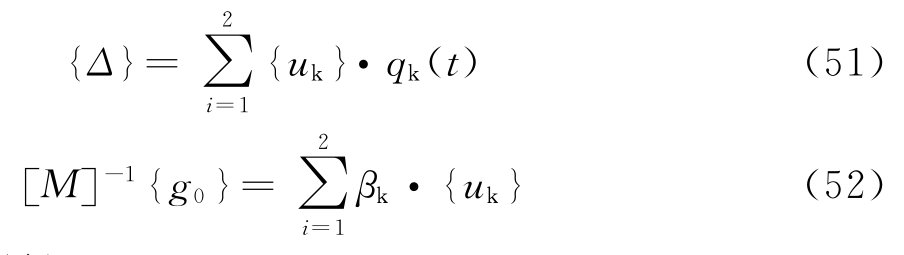 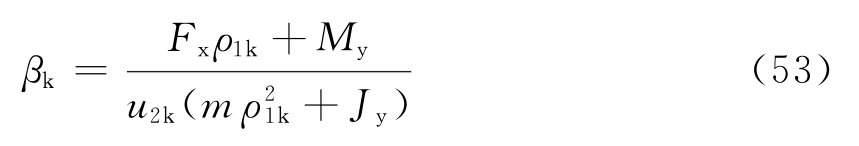 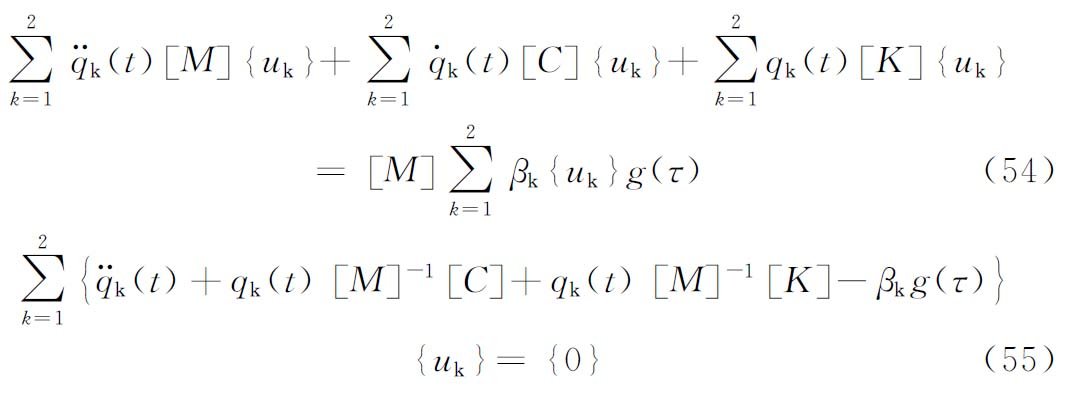 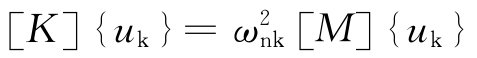 ; ;可得 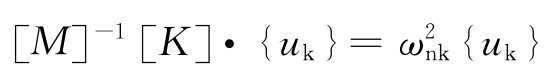 ,并有下式: ,并有下式:
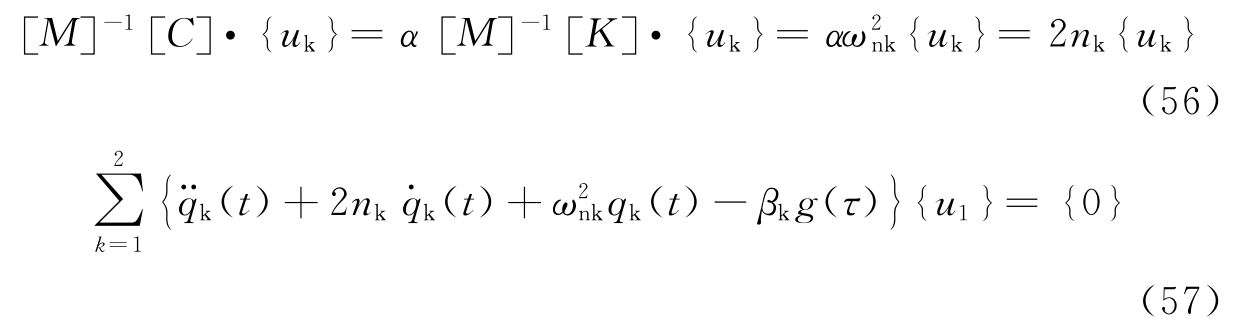 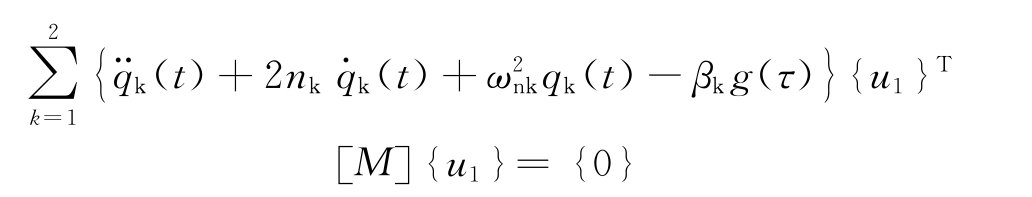 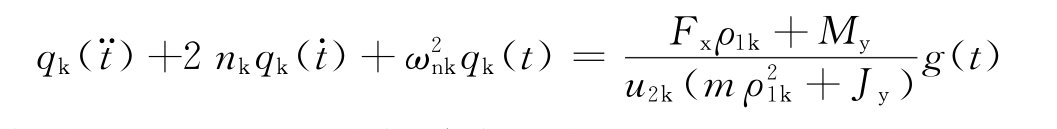 当扰力时间函数为简谐时,g(t)=sinωt,其解为: 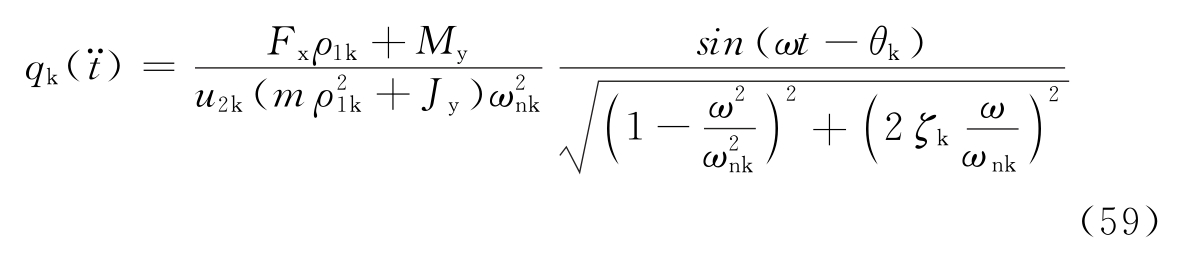 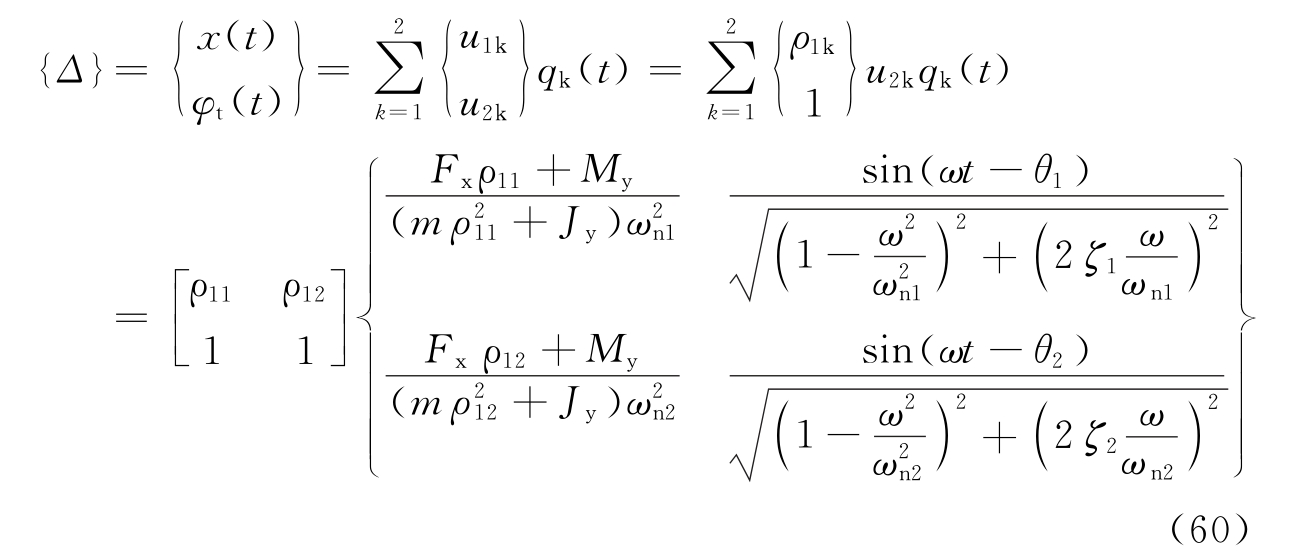 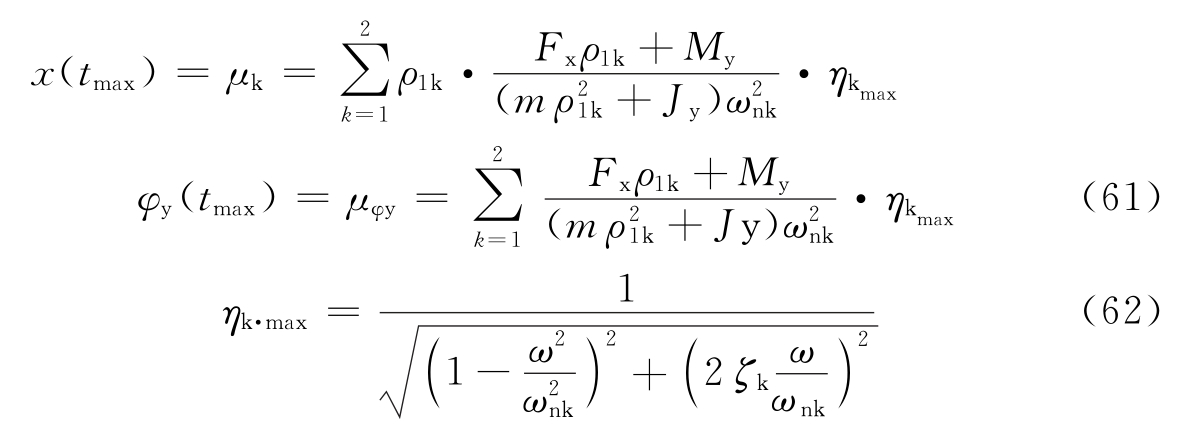
4.1.3 本条的传递率为主动隔振体系在扰力作用下的输出振动线位移与静位移之比,静位移为振动荷载幅值除以隔振器静刚度得到的等效静位移。附录A中给出五种脉冲荷载在不同阻尼比工况下的传递率,方便工程设计使用。
4.1.5 在隔振基础上任意点的振动幅值的计算方法,特别是扰力(扰力矩)的工作频率均不相同时,均采用振动幅值绝对值之和,这是既简便又比较安全的。当扰力(扰力矩)的工作频率一致但是作用时间有相位差时,如采取时程分析时,要考虑振动效应相位差的影响;简化起见,也可采用本条第3款规定包络计算。
|
Powered by Discuz! X3.5
© 2001-2025 Discuz! Team.